Etude de la porosité et de la perméabilité
La Terre et l'atmosphère possédent 1.385·109 km3 d'eau, quantité qui n'a quasiment pas varié depuis la création du Globe. Cependant les océans mobilisent représente 97,5% des réserves d'eau du globe, l'eau douce n'en représente que 2.5% dont les 4/5 (2%) sont situés dans les glaciers et les banquises. Le reste (0.5%) est essentiellement constitué par les eaux souterraines, les lacs, les fleuves et rivières, l'humidité des sols.
Les eaux souterraines représentent la quasi-totalité (97 à 98%) des réserves d'eau douce stockées.
Mais qu'est ce qu'un réservoir souterrain ? une citerne ?
En fait les roches peuvent contenir du liquide ! Pour le démontrer vous pouvez réaliser cette expérience fort simple :
- Placez différentes roches dans une étuve pendant plusieurs heures pour les sécher. Puis pesez les avec précision.
- Plongez les roches dans l'eau pendant une heure minimum. Retirez les et enlevez l'excès d'eau en les secouant. Pesez-les de nouveau.
- Laissez les roches dans l'eau pendant plusieurs jours. Pesez-les de nouveau.
- Que pouvez-vous conclure de vos résultats ?
Dans une roche, l'eau occupe les espaces existant entre ses constituants sous forme de pores, interstices ou de fissures.
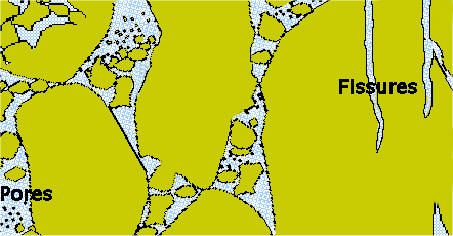
Notion de porosité et de perméabilité
L'eau peut, selon le type de roche, pénétrer : c'est la porosité de la roche. L'eau peut aussi traverser complètement la roche : c'est la perméabilité de la roche.
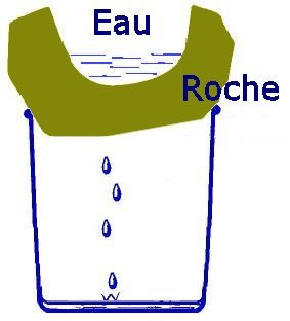
Ces deux paramètres fondamentaux représentent donc :
- la porosité : correspondant au volume relatif des vides présents dans la roche (nombre sans dimension),
- la perméabilité : mesure de l'aptitude d'une roche à se laisser traverser par l'eau.
-
Comparaison de la porosité de deux roches :
Mettre quelques gouttes d'eau sur différentes roches, et observer.
En déduire la porosité de ces roches.
-
Comparaison de la perméabilité de deux roches :
La perméabilité correspond à la vitesse à laquelle l'eau circule au sein de la roche.
Très simplement il est possible de comparer la perméabilité de deux roches sédimentaires. Il s'agit de mettre dans deux entonnoirs deux mêmes volumes de roche et de verser le même volume d'eau, enfin de comparer après un temps donné le volume d'eau ayant traversé ces roches.
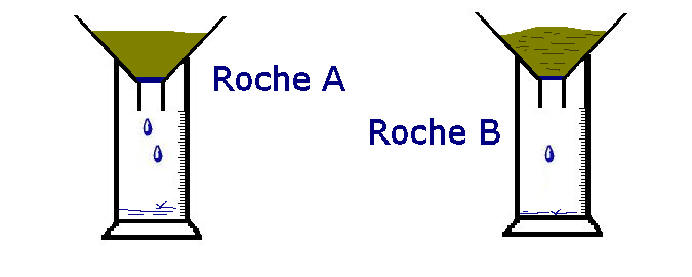
Mesure de la porosité
La porosité totale (pt) se définit de la façon suivante :
Pt (%) = Volume des vides / volume total de la roche x 100
Cette porosité totale peut se décomposer en :
- pe (porosité efficace) : c'est la quantité d'eau de gravité contenue dans une roche, ou quantité d'eau mobile.
- cr (capacité de rétention) : c'est la quantité d'eau liée aux particules et/ou capillaire.
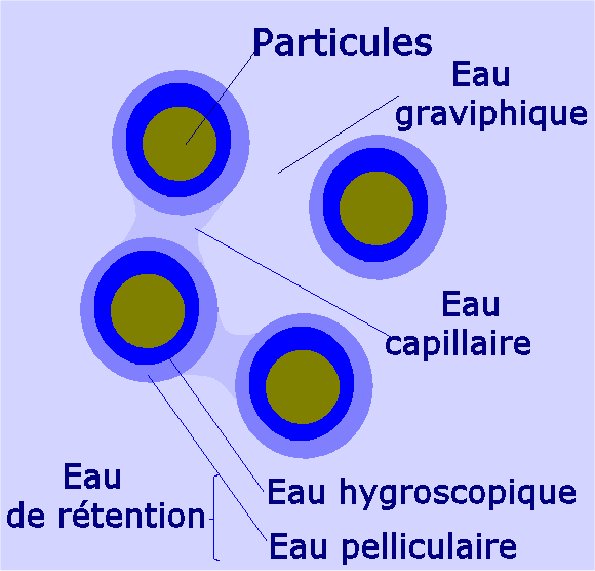
Plus la particule est de petite dimension, plus la composante "pe" diminue et donc plus la composante "cr" augmente.
| Roches poreuses | pt (%) | pe (%) |
| Sable et gravier | 25 à 40 | 15 à 25 |
| Sable fin | 30 à 35 | 10 à 15 |
| Argile | 40 à 50 | 1 à 2 |
| Craie | 10 à 40 | 1 à 5 |
| Calcaire (fissuré) | 1 à 10 | 10 à 50 |
-
Mesurer la porosité d'une roche : Pt (%) = Volume des vides / volume total de la roche x 100
Il est possible de déterminer le volume d'eau contenu dans une roche en pesant la roche avant et après un séjour prolongé dans l'eau. La différence mesurée en gramme est convertie en volume 1g = 1 cm3, ce volume représente le volumes des vides.
Il est possible de mesurer le volume total de la roche en mesurant la quantité d'eau déplacée lors de son immersion.
-
Autre méthode
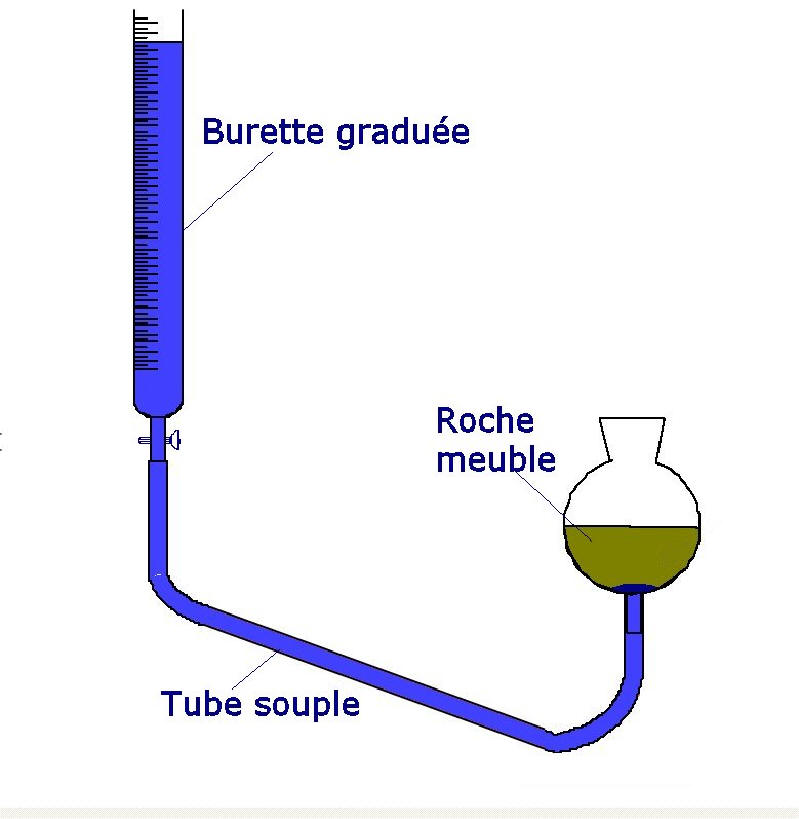
Réaliser le montage ci-dessus. Ouvrir le robinet. L'eau va ainsi, par gravité, monter dans la roche meuble. Quand l'eau arrive au sommet du sol, fermer le robinet et lire le volume d'eau écoulée et qui a servi à remplir tous les espaces vides du sol. Si vous connaissez le volume de la roche meuble, vous pouvez déterminer la porosité totale.
Mesure de la perméabilité
L'écoulement des eaux souterraines est régi par la loi de Darcy établie expérimentalement en 1856 (définition de la perméabilité).
a- Dispositif expérimental :
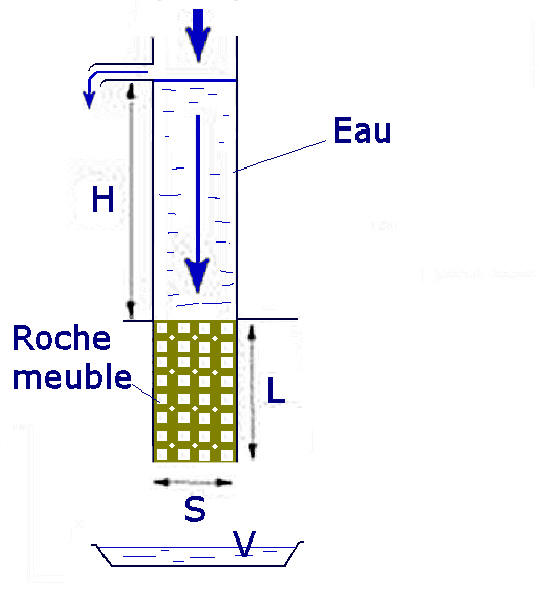
Lorsque le milieu est saturé en eau, on a :
débit d'entrée Qe = débit sortie Qs = Q
L'équation de Darcy s'écrit :
Q = k.S.∆H/L
Donc le débit Q (m3.s-1) est proportionnel à S et ∆H et inversement proportionnel à L.
k correspond au coefficient de perméabilité de Darcy = perméabilité (m.s-1)
S = surface (m²)
∆H = perte de charge (m)
K ( m/s ) = Q / S x I
Q = débit ( m3/s ), S = surface (m2) et I le gradient hydraulique.
le gradient hydraulique I = ∆H / L
De façon simple, on peut calculer k = L X V / (L + H) x V
Remarque : la perméabilité de Darcy est utilisée uniquement quand on s'intéresse à l'exploitation de nappes libres.
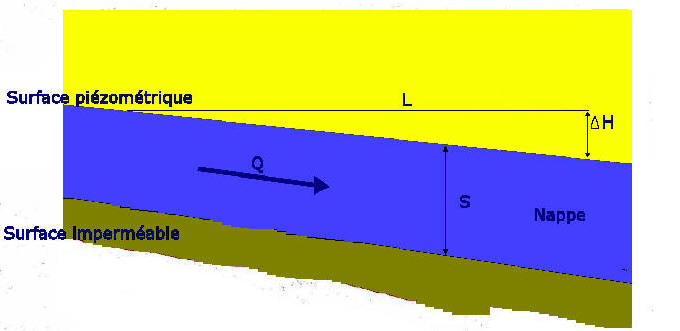
∆H = perte de charge (m)
I =∆H/L
Loi de Darcy Q = k.S.∆H/L
Pour une longueur d'aquifère L et pour une section supposée constante S
Quelques résultats :
| Roches poreuses |
porosité totale (%) |
perméabilité (m/Jour) |
| Sable et gravier | 25 à 40 | 1000 à 10 |
| Sable fin | 30 à 35 | 100 à 0,1 |
| Argile | 40 à 50 | < 0,1 |
| Craie | 10 à 40 | 100 à 1 |
| Calcaire (fissuré) | 1 à 10 | < 1 |

